Neuronale Netze¶
Neuronale Netze¶
Künstliche neuronale Netze sind Informationsverarbeitende Systeme, deren Struktur und Funktionsweise an das Nervensystem und speziell an das Gerhin von Menschen und Tieren errinnert. Ein neuronales Netz besteht oft aus einer großen Anzahl einfacher parallel arbeitender Einheiten, den sogenannten Neuronen. Diese Neuronen senden sich Informationen, in Form von Aktivierungssignalen, über gewichtete Verbindungen zu. Ein neuronales Netz ist in mehreren Schichten angeordnet: der Inputschicht, der Outputschicht und den dazwischen liegenden “Hidden Layers”.
Betrachten wir ein Beispiel zum Thema Immobilienpreise:

Am Beispiel zur Errechnung von Hauspreisen, lässt sich ein neuronales Netz verdeutlichen. Dabei haben wir eine Reihe von Inputs. Dies sind z.B. Merkmale wie die Anzahl der Schlafzimmer, das Vorhandensein eines Swimmingpools (Ja oder Nein), gibt es einen Garten und die Größe der Wohnfläche. Die Inputs sind dann mit den dazwischen liegenden Hidden Layern an verschiedenen Punkten verbunden. Die Hidden Layer können wiederum mit anderen Layern verbunden sein. Am Ende entsteht so der Output. In unserem Beispiel ist das der errechnete Hauspreis. Jeder Hidden Layer entsteht aus einer anderen Kombination der Inputs. Daraus ergeben sich Kombinationen von Kombinationen usw. Die dahinter liegende Funktion ist sehr komplex. Deshalb wird in diesem Zusammenhang auch von einer “Blackbox” gesprochen. Da nur mit enormen Aufwand jede Rechenoperation nachvollzogen werden könnte. Klassische neuronale Netze funktionieren in dem hier skizzierten Hintergrund sehr gut. Doch wie sieht es mit der Verarbeitung von Bildern aus? Hier stößt ein herkömmliches neuronales Netz an seine Grenzen. Bei einem Bild mit beispielsweise 7 Millionen Pixeln, hätten wir eine enorme Anzahl an Inputs mit einer ebenso großen Anzahl an Layern. Dies ist selbst mit riesen Rechenclustern kaum zu stemmen. Hierfür muss eine andere Methode genutzt werden [3,4,7] :
Convolutional Neural Networks (CNN) / Deep Learning¶
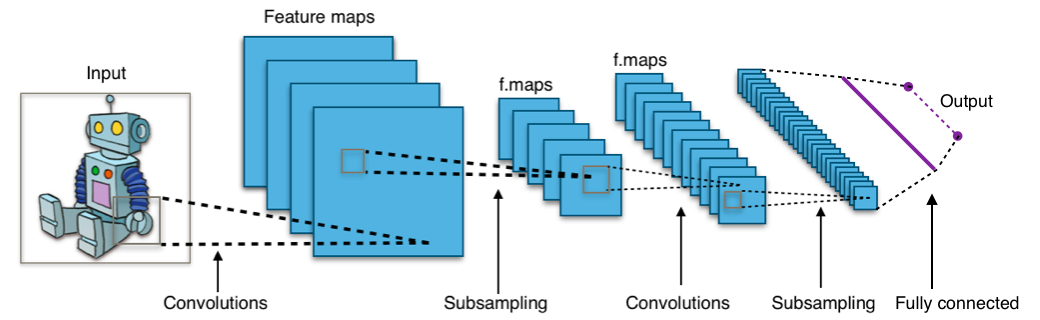
Convolutional Neural Networks (CNN) extrahieren lokalisierte Merkmale aus Eingangsbildern und falten diese Bildfelder mittels Filtern auf. Der Eingang zu einer Faltungsschicht ist ein m x m x r Bild, wobei m die Höhe und Breite des Bildes ist und r die Anzahl der Kanäle ist. Beispielsweise hat ein RGB-Bild r = 3 Kanäle. Diese Daten werden nun durch mehrere Schichten übergeben und immer wieder neu gefiltert und unterabgetastet [8,10] .
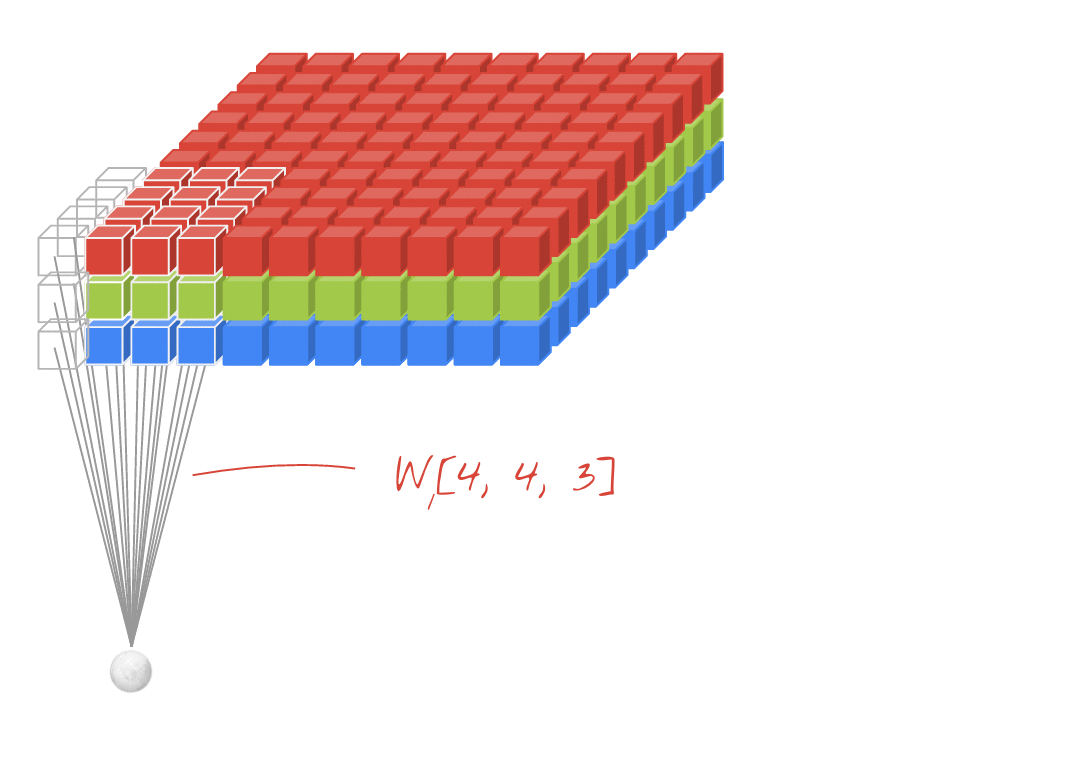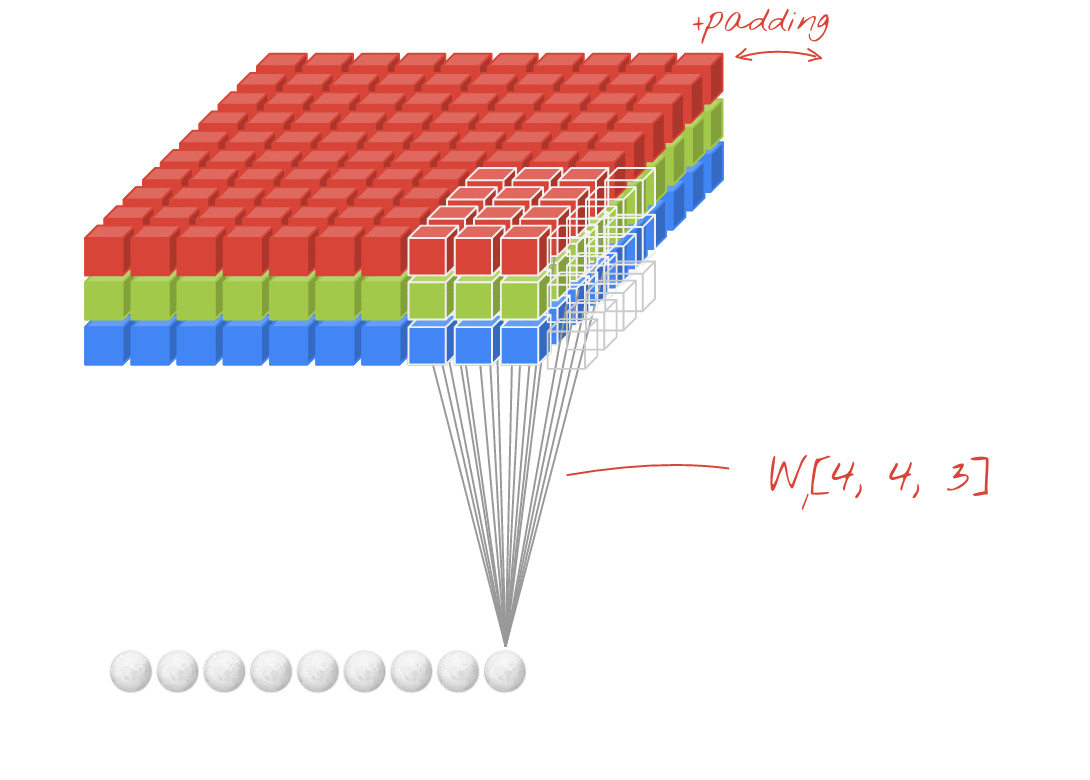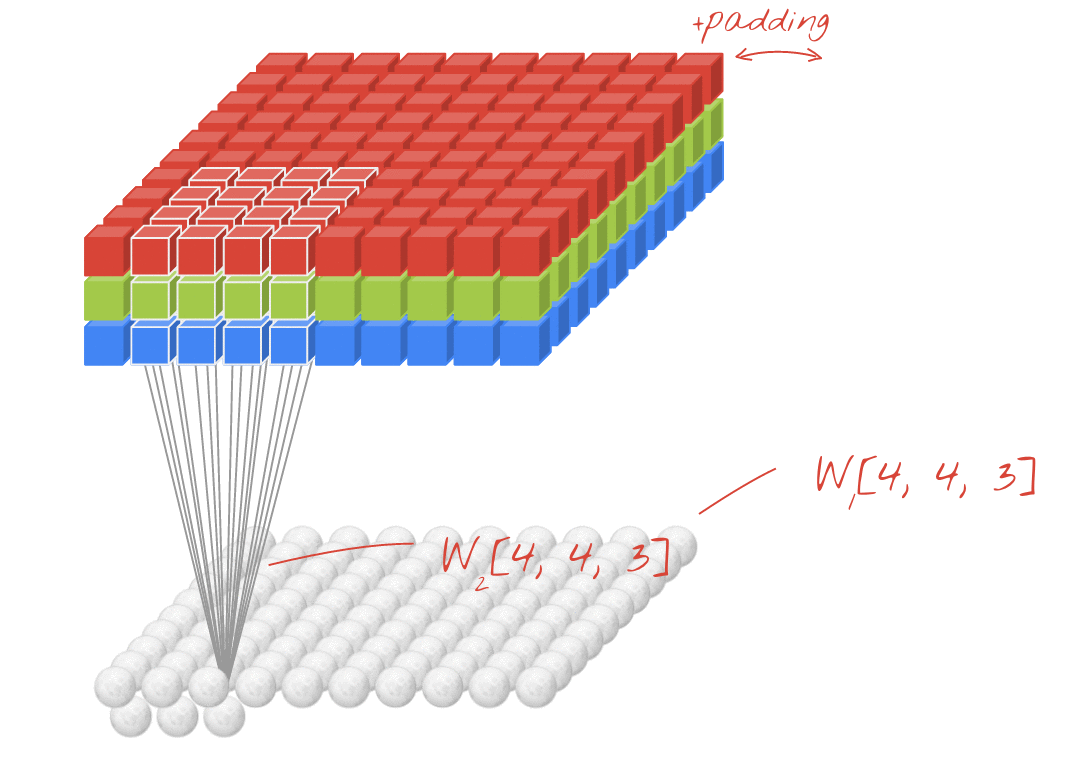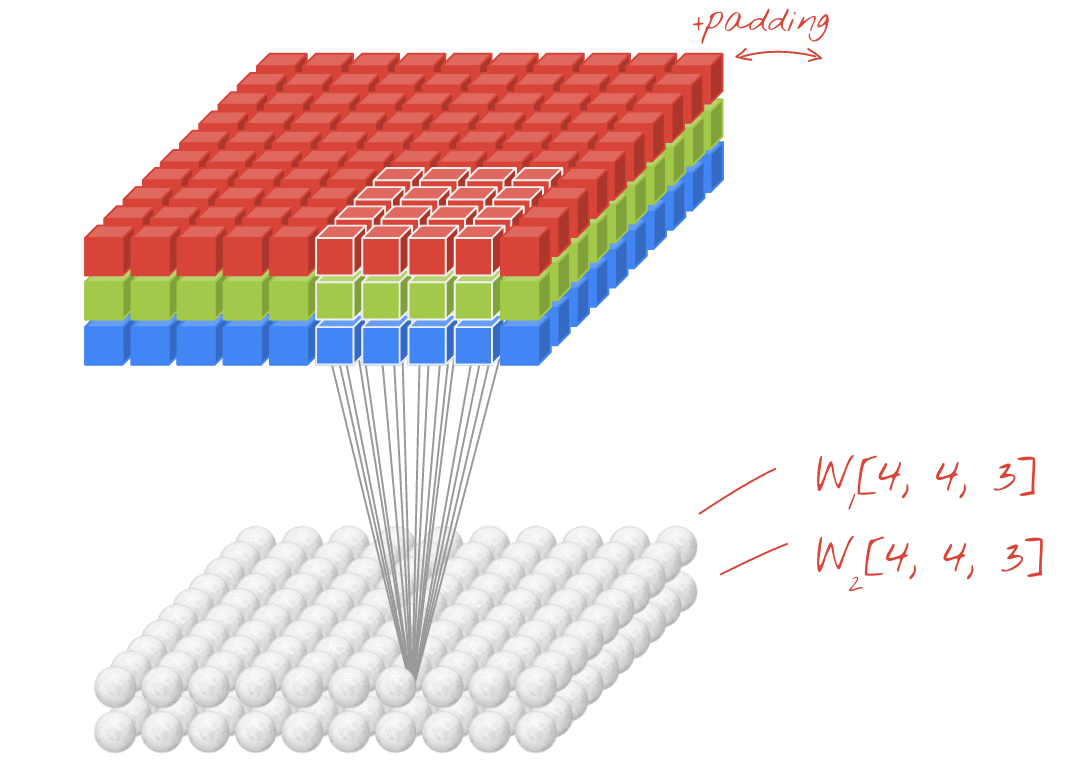
Die letzte Schicht gibt eine Punktzahl für jede Bildklasse aus, die die Wahrscheinlichkeit der Eingabe dieser Klasse darstellt. Einige der verwendeten Filter werden im Folgenden kurz erläutert [9] .
Aktivierungsfunktionen¶
In dieser Arbeit kommen mittels der TensorFlow Implementierungen die Aktivierungsfunktionen Sigmoid und ReLu zum Einsatz.
Die Sigmoidfunktion sieht folgendermaßen aus:
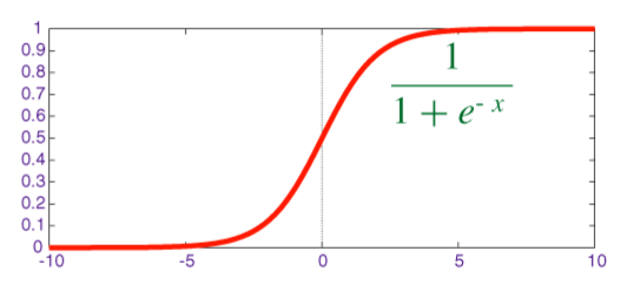
Die ReLu (Rectified Linear Unit) Funktion stellt die heutzutage in CNN bevorzugte Aktivierungsfunktionen dar:
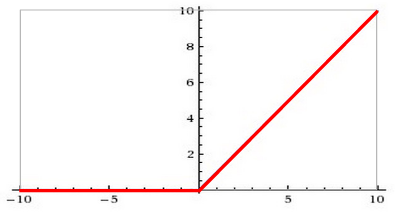
Die Sigmoidfunktion deckt nur einen Bereich zwischen [0,1] ab. Die ReLu jedoch einen Bereich zwischen [0,∞]. Deswegen kann die Sigmoidfunktion benutzt werden, um Wahrscheinlichkeiten zu modellieren. Mittels ReLu können jedoch alle positiven reellen Zahlen modelliert werden. Der wesentliche Vorteil der ReLu Funktion besteht darin, dass sie beim Berechnen von CNNs keine Probleme mit dem “schwinden” des Gradienten haben, wie es bei der Sigmoidfunktion auftreten kann. Des Weiteren hat sich heraus gestellt, dass CNNs mittels ReLu effizienter trainiert werden können [1,5,6] .
MaxPooling¶
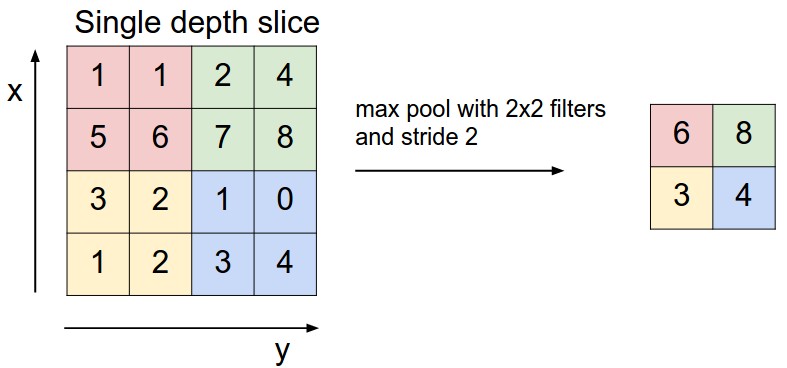
Max-Pooling ist ein Beispiel-basierter Diskretisierungsprozess. Ziel ist es, eine Eingabedarstellung (Bild-, Hidden-Layer-Ausgangsmatrix etc.) abzutasten, die Dimensionalität zu reduzieren und Annahmen über die in den Unterregionen enthaltenen Features zu machen. Durch Max-Pooling wird die Anzahl der zu erlernenden Parameter - und somit auch der Rechenaufwand - reduziert.
Flatten und Dense¶
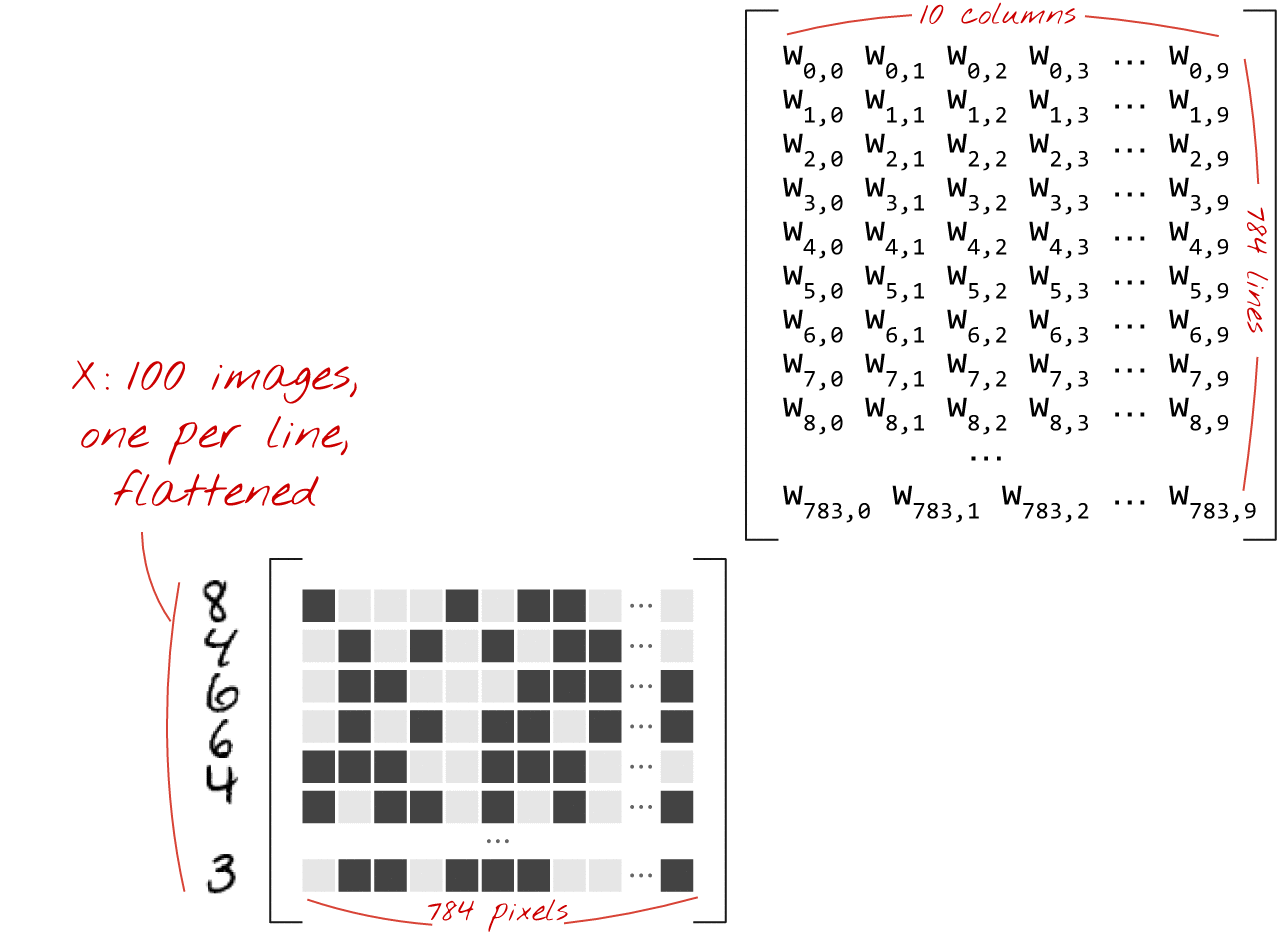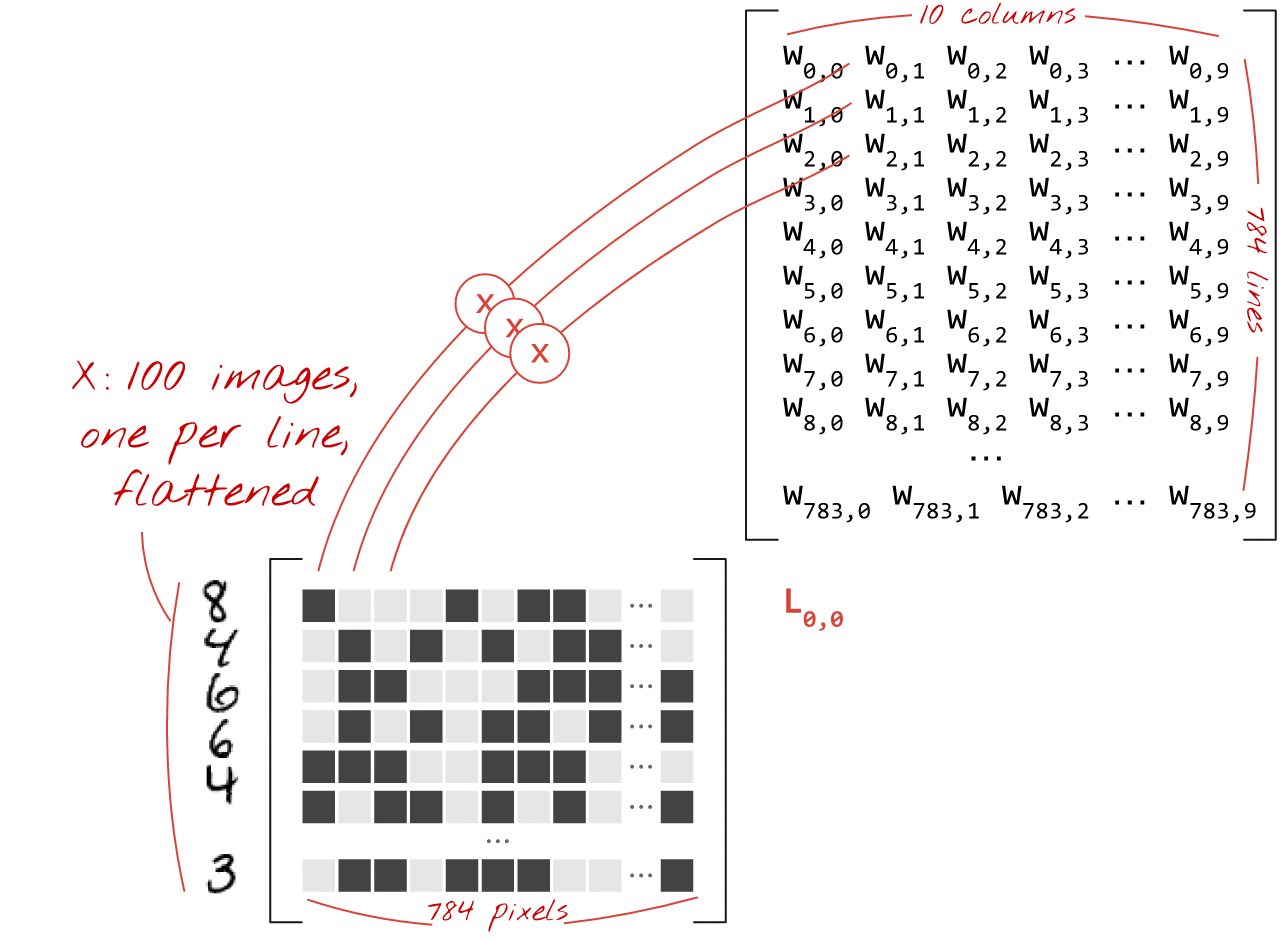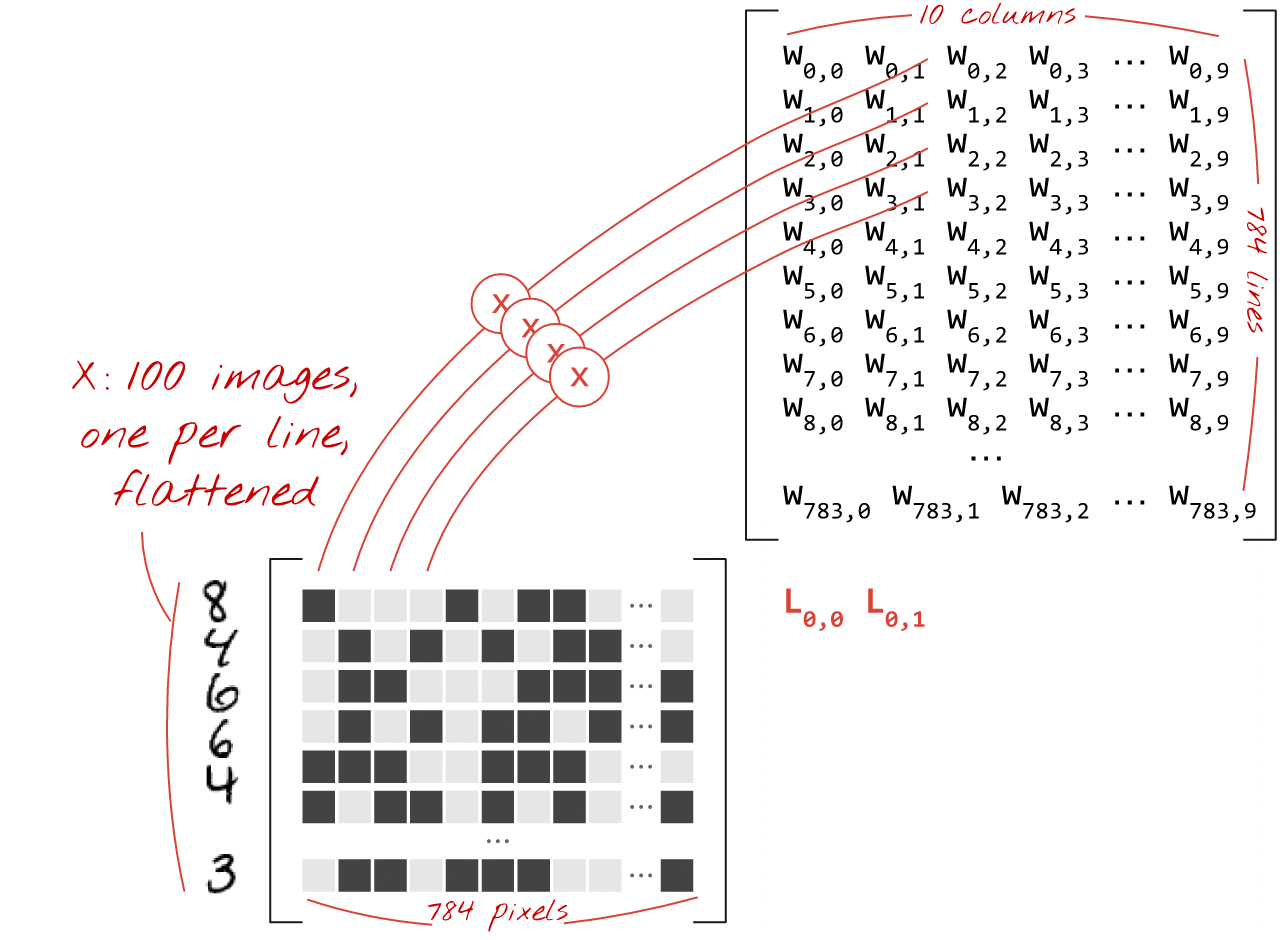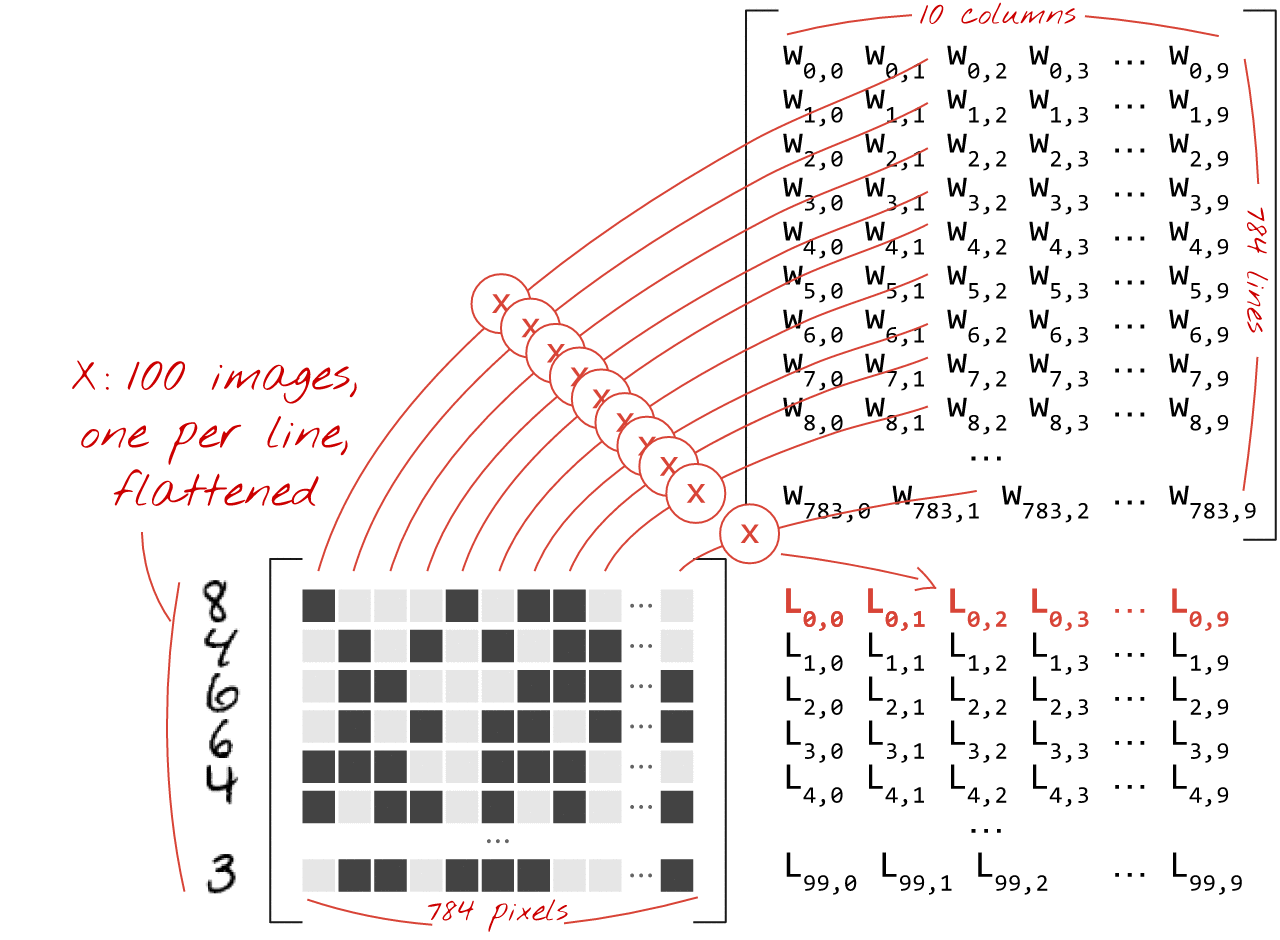
Der Klassifizierer ist der letzte Schritt in einem CNN. Dieser wird als Dense Layer bezeichnet, welcher ein gewöhnlicher Klassifizierer für neuronale Netze ist. Der Dense Layer tastet sich von der Poolingschicht aus abwärts. In dieser Schicht ist jeder Knoten mit jedem Knoten in der vorhergehenden Ebene verbunden. Wie jeder Klassifizierer, braucht dieser individuelle Features. Er benötigt also einen Feature Vector. Dazu muss der mehrdimensionale Output aus den Convolutions in ein eindimensionalen Vector überführt werden. Diesen Vorgang nennt man “Flattening” [12] .
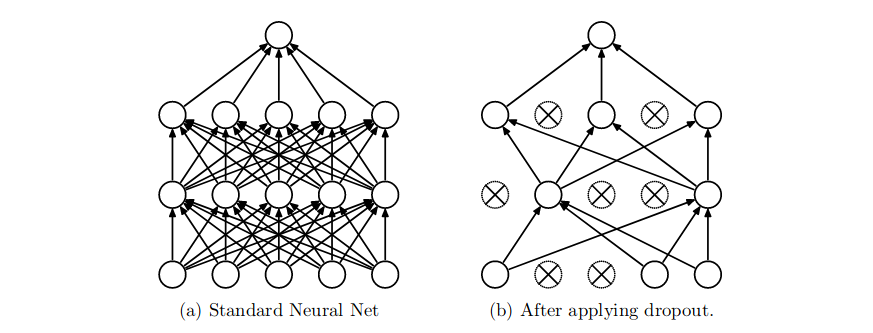
Dropout¶
Overfitting kann bei CNNs mit einer großen Anzahl von Parametern ein enormes Problem sein. Dropout ist eine Technik, um dem entgegen zu wirken. Die Idee ist folgende: Während des Trainings werden zufällig Units und ihre Eingangs- und Ausgangsverbindungen aus dem Netzwerk entfernt (“drop out”). Dies hält die Units davon ab, dass sie sich zu sehr “co-annähern”. Die Units sollen sich nach Möglichkeit individuell von einander unterscheiden, damit ihre Merkmale zu Tage kommen.
Dropout anzuwenden bedeutet, dass “ausgedünnte” Proben des Netzwerks erstellt werden. Das ausgedünnte Netzwerk besteht aus allen Units die den Dropout überlebt haben. Ein neuronales Netz aus n Units kann als eine Sammlung von 2^n möglichen ausgedünnten Netzen angesehen werden [12] .