Empfohlene Unterrichtsinhalte als Vorbereitung für dieses Thema: 03-01 (Indexing und Slicing), 03-02 (Bedingungen), 03-03 (Schleifen), 05-01 (Funktionen), 05-02 (None), 06-02 (Debugging), 10-01 (String formatting)

Einführung in die computerlinguistische Programmierung mit Python

11-02: Rekursion II ↗️

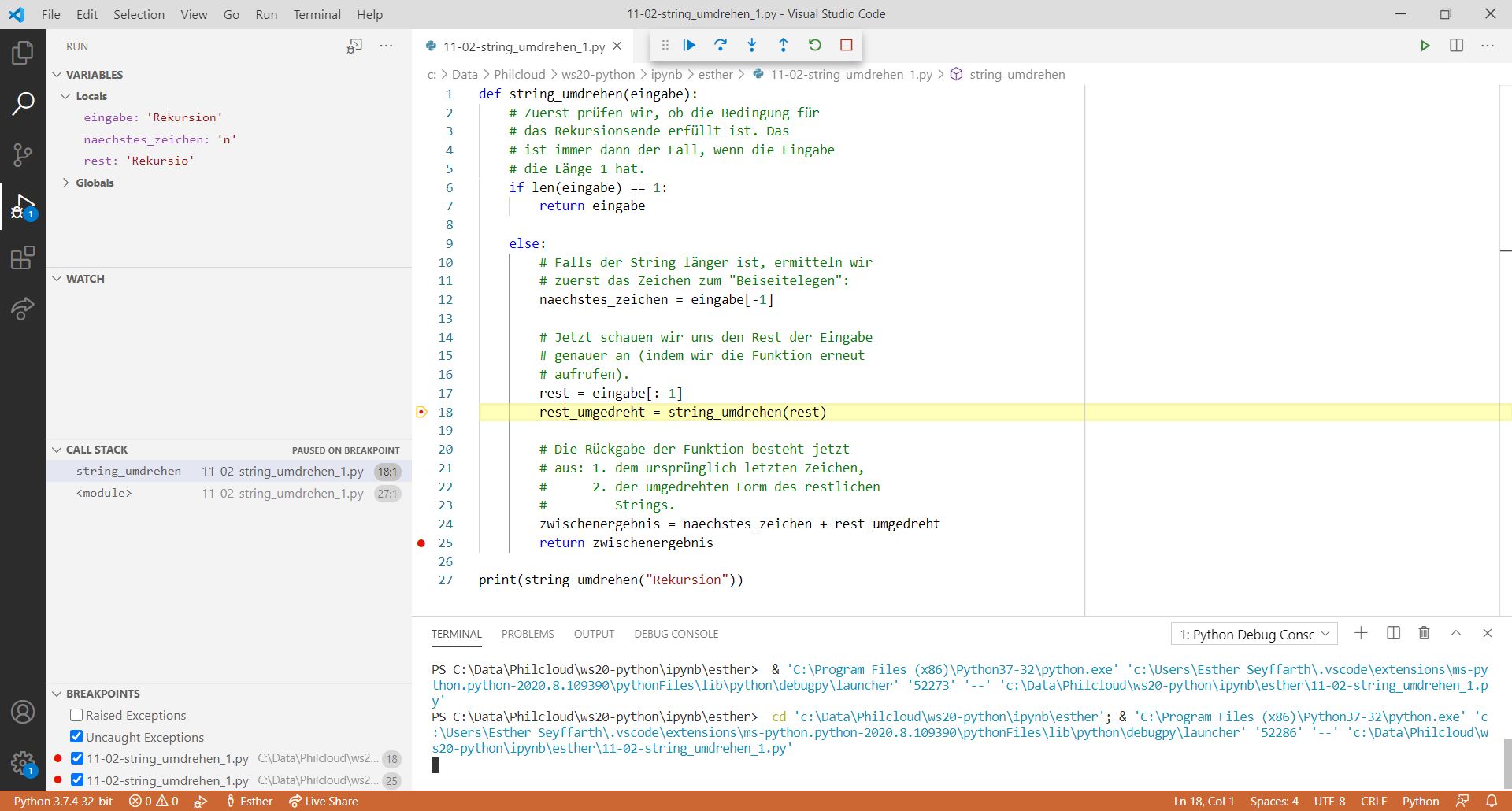
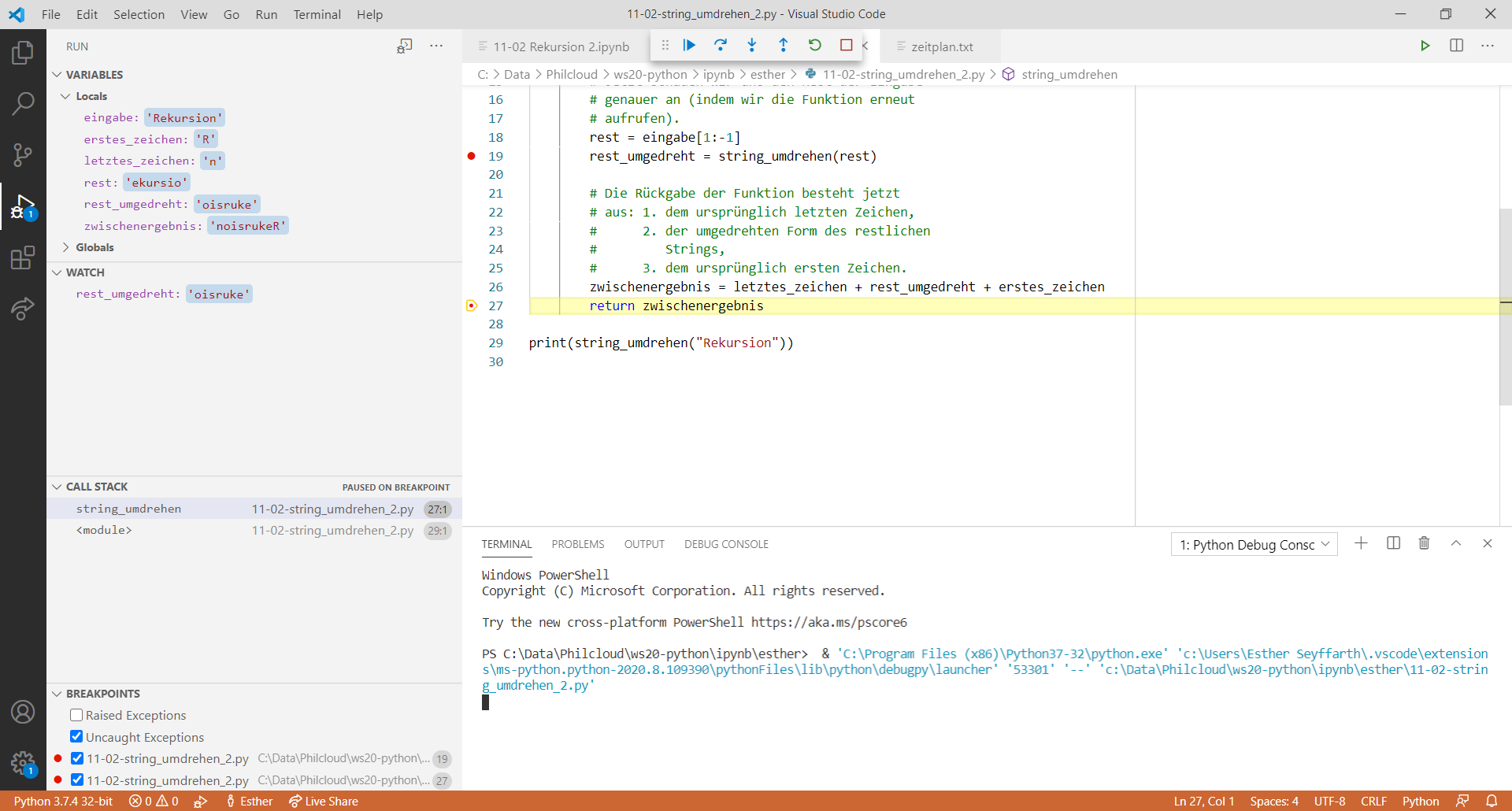
Nachdem wir die Grundlagen der Rekursion kennengelernt haben, schauen wir uns jetzt noch einige weitere Beispiele an. Diesmal verfolgen wir den Flow des Programms mit dem Debugger von VSCode, um genau zu sehen, wie die Programme ausgeführt werden.

Wir können viele Probleme mit Rekursion lösen: Immer dann, wenn ein Problem in Teilprobleme zerlegt werden kann, ist Rekursion eine Möglichkeit. Zum Beispiel können wir einen beliebigen String umdrehen, indem wir zuerst das letzte Zeichen ermitteln und uns dann um den restlichen String (vom Anfang bis einschließlich Index -2) kümmern.

Für den String "Rekursion" würden wir die folgenden Schritte durchlaufen:

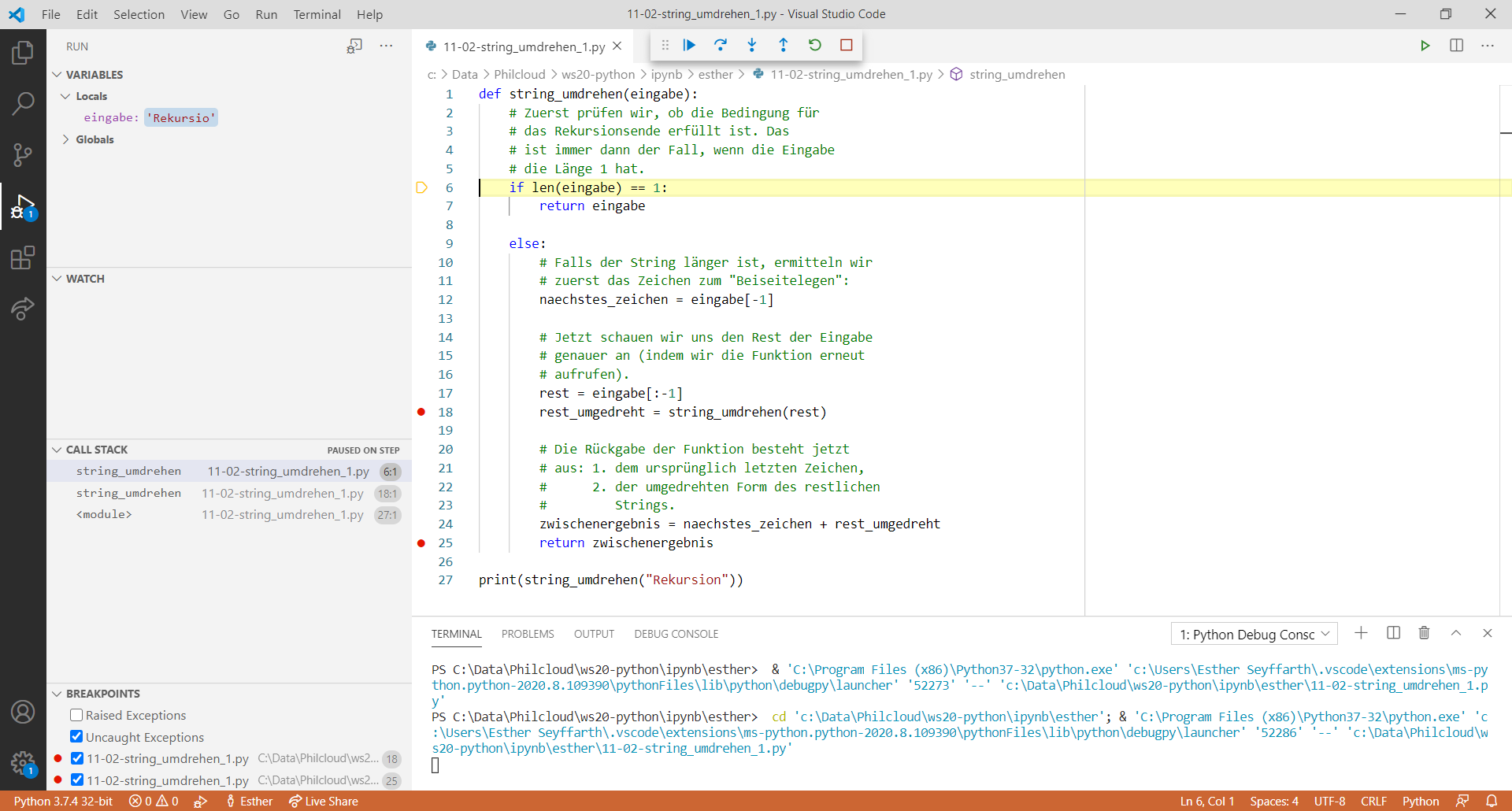
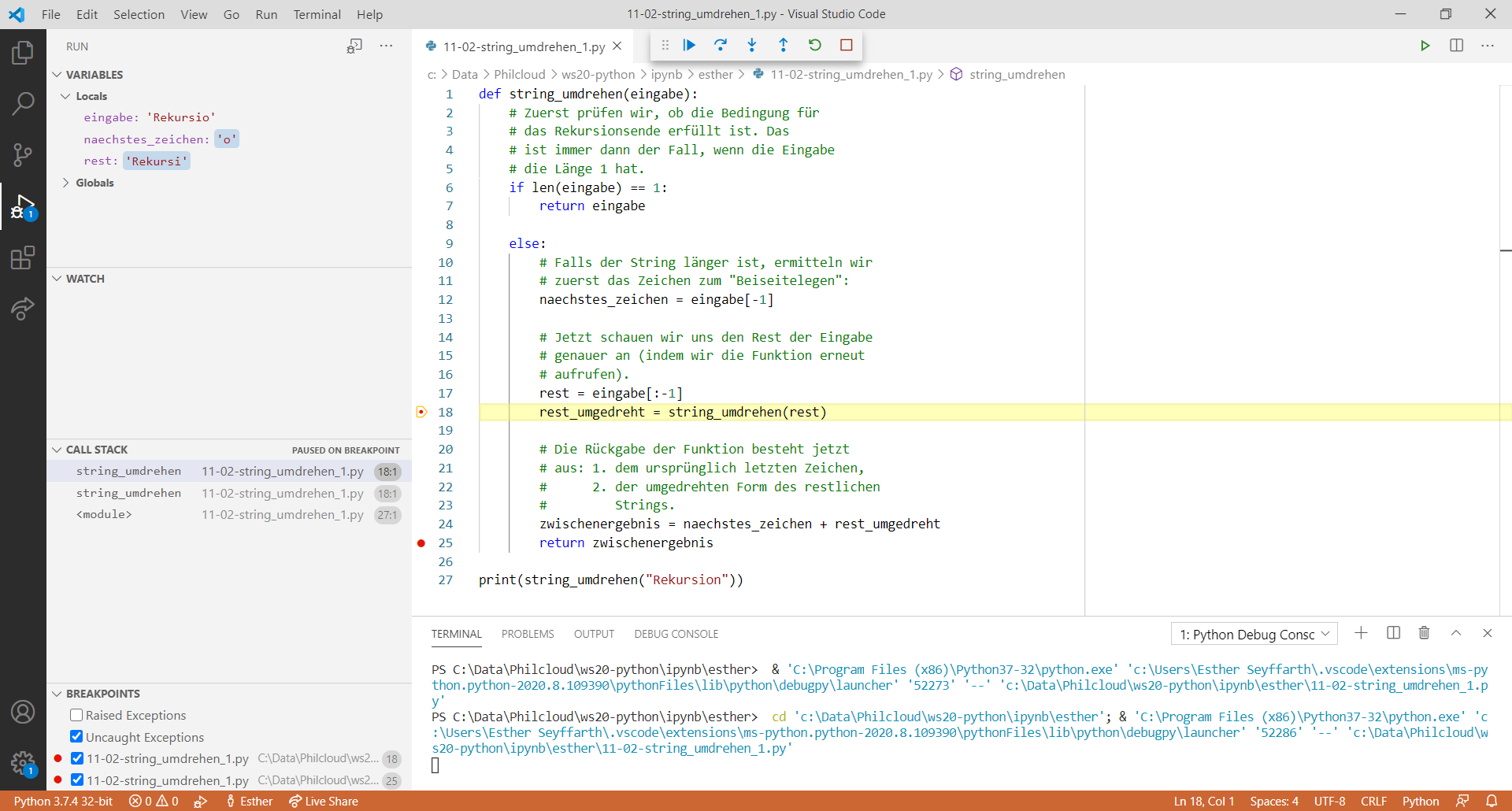
1. "n" beiseite legen; als nächstes den String "Rekursio" betrachten.
2. "o" beiseite legen; als nächstes den String "Rekursi" betrachten.
3. "i" beiseite legen; als nächstes den String "Rekurs" betrachten.
4. .........
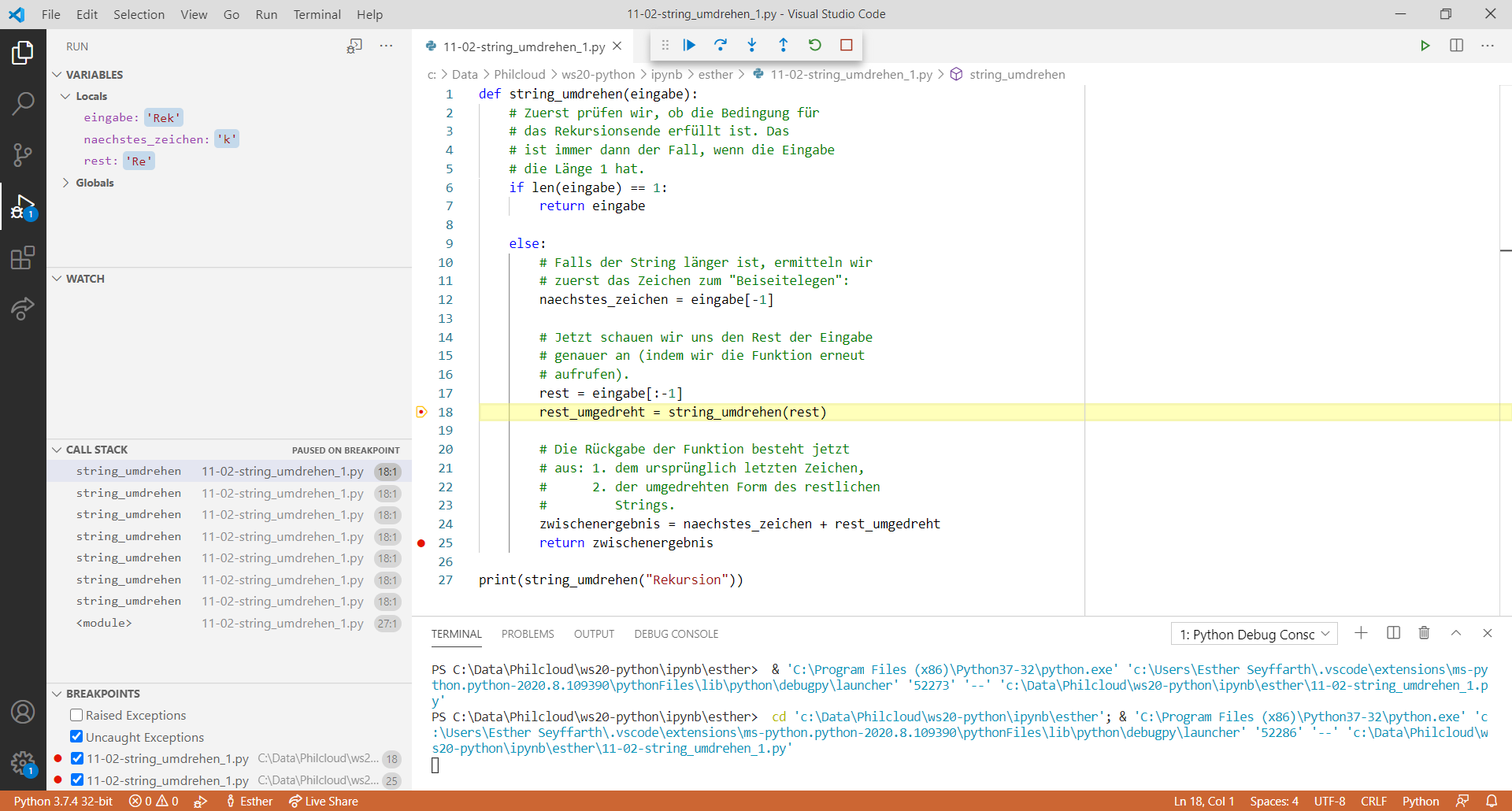
5. "e" beiseite legen; als nächstes den String "R" betrachten.
6. "R" muss nicht umgedreht werden! Rekursionsende!

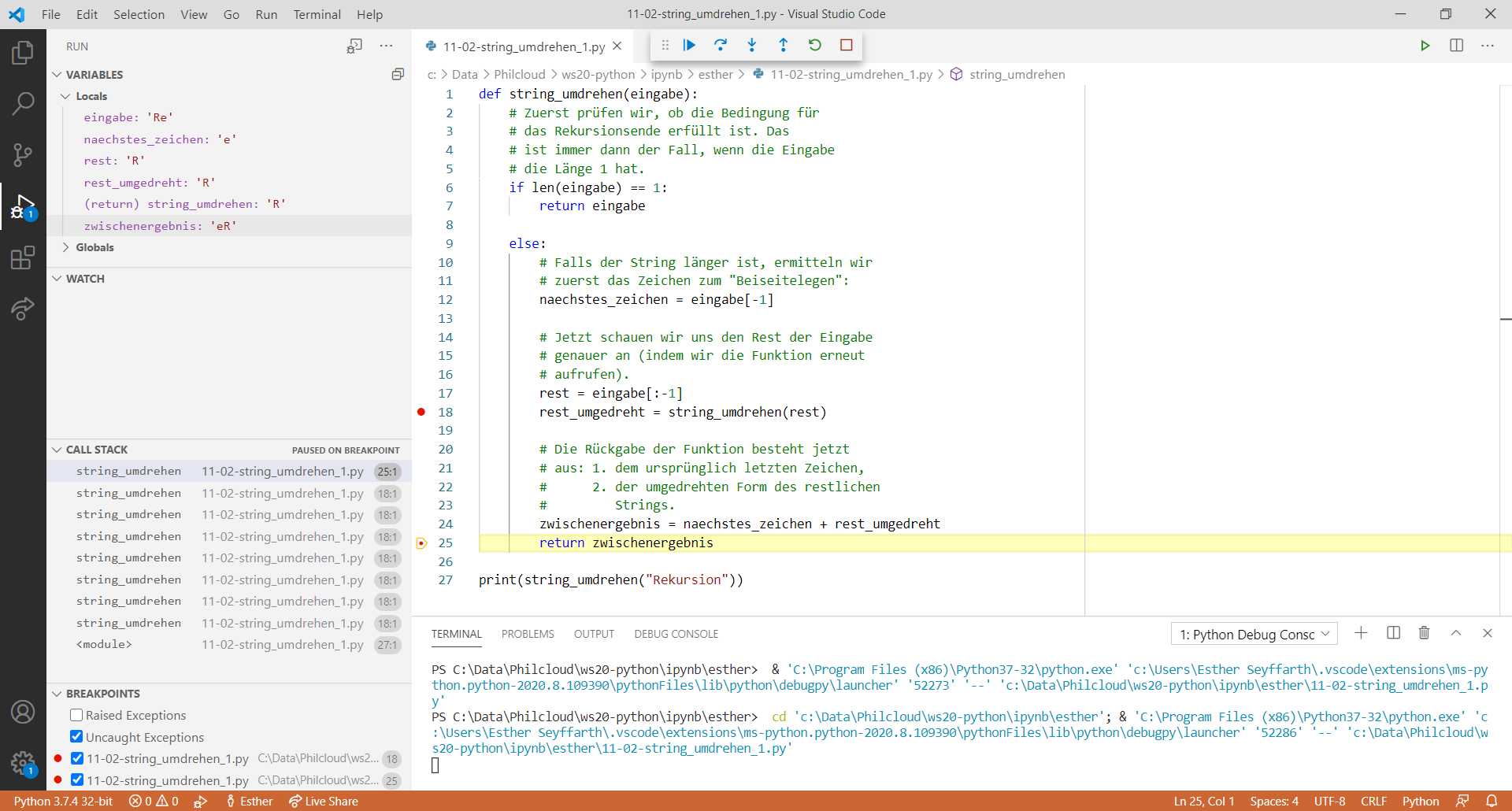
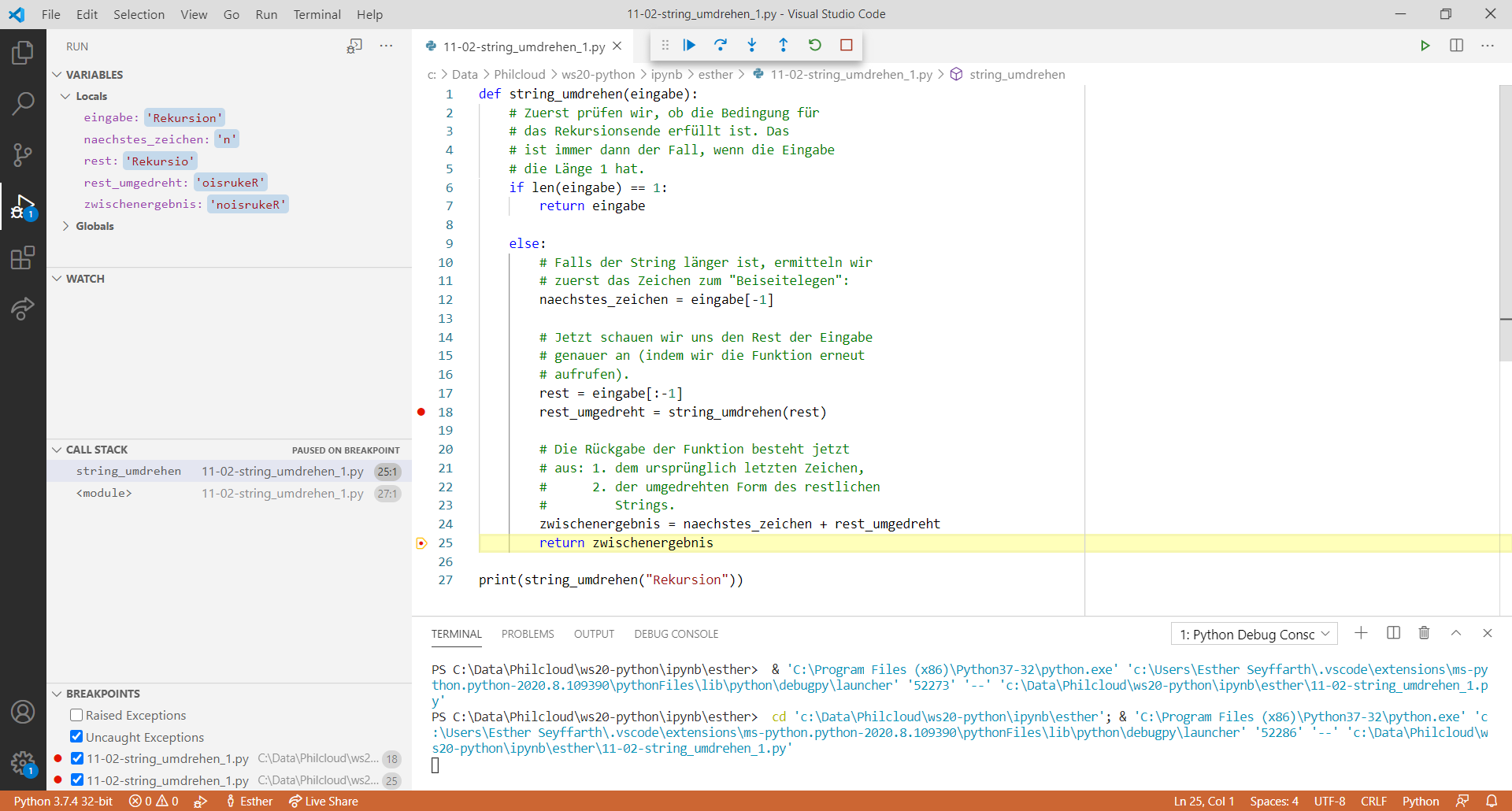
Nachdem wir beim letzten Schritt ankommen, können wir anfangen, das Ergebnis zusammenzufügen. Dafür nehmen wir jeweils das zuletzt beiseitegelegte Zeichen (hier: das "e") und konkatenieren es mit dem aktuellen Zeichen (hier: das "R"). Dieses Zwischenergebnis hängen wir dann an das direkt davor beiseitegelegte Zeichen an, in diesem Fall an das "k". Dabei erhalten wir den umgedrehten Teilstring "keR". Wir können jeden Schritt nacheinander durchführen, bis wir schließlich das Teilergebnis "oisrukeR" an das zuerst beiseitegelegte Zeichen "n" anfügen. Danach ist die Aufgabe erfüllt und die Rekursion beendet.

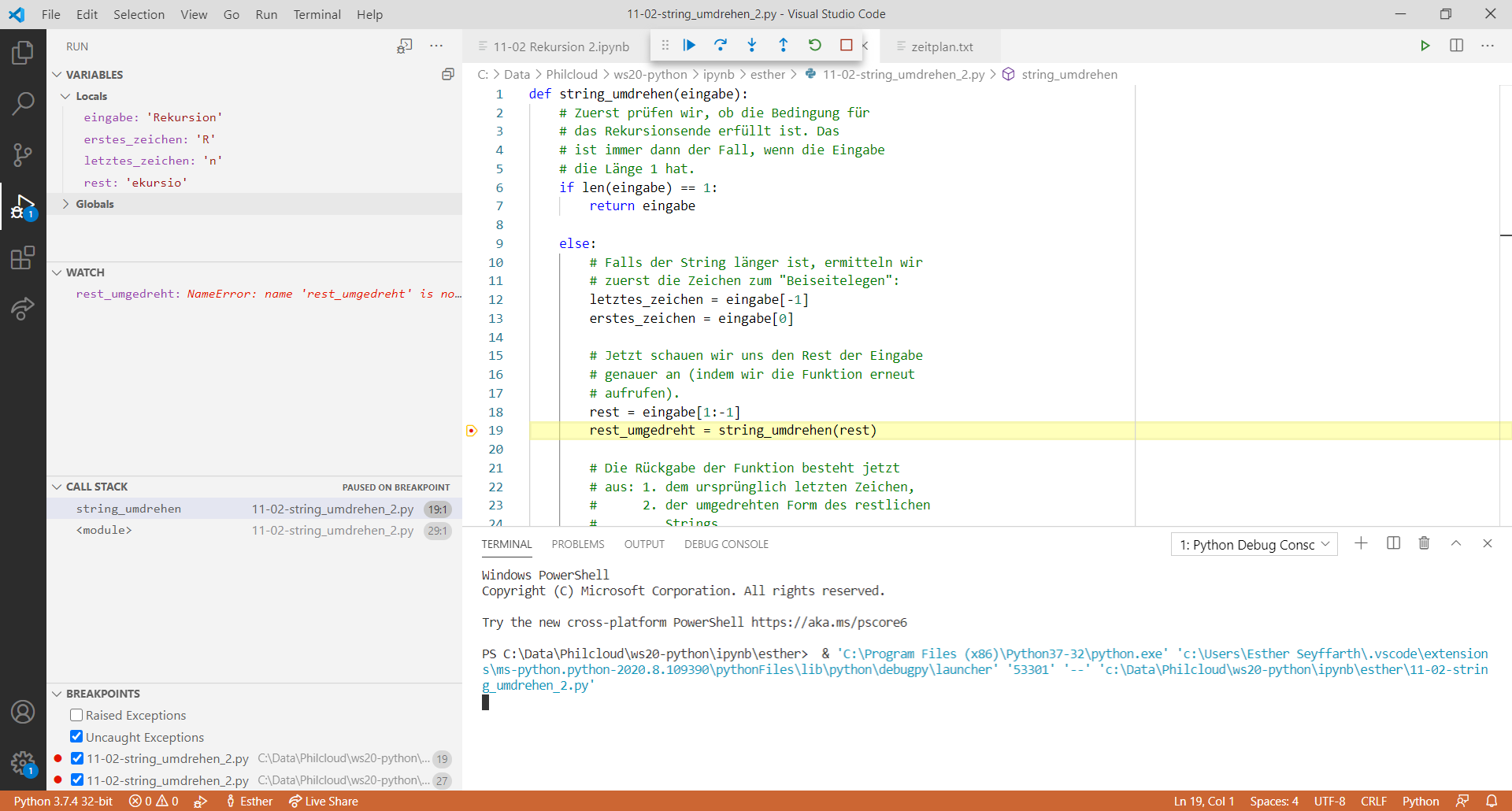
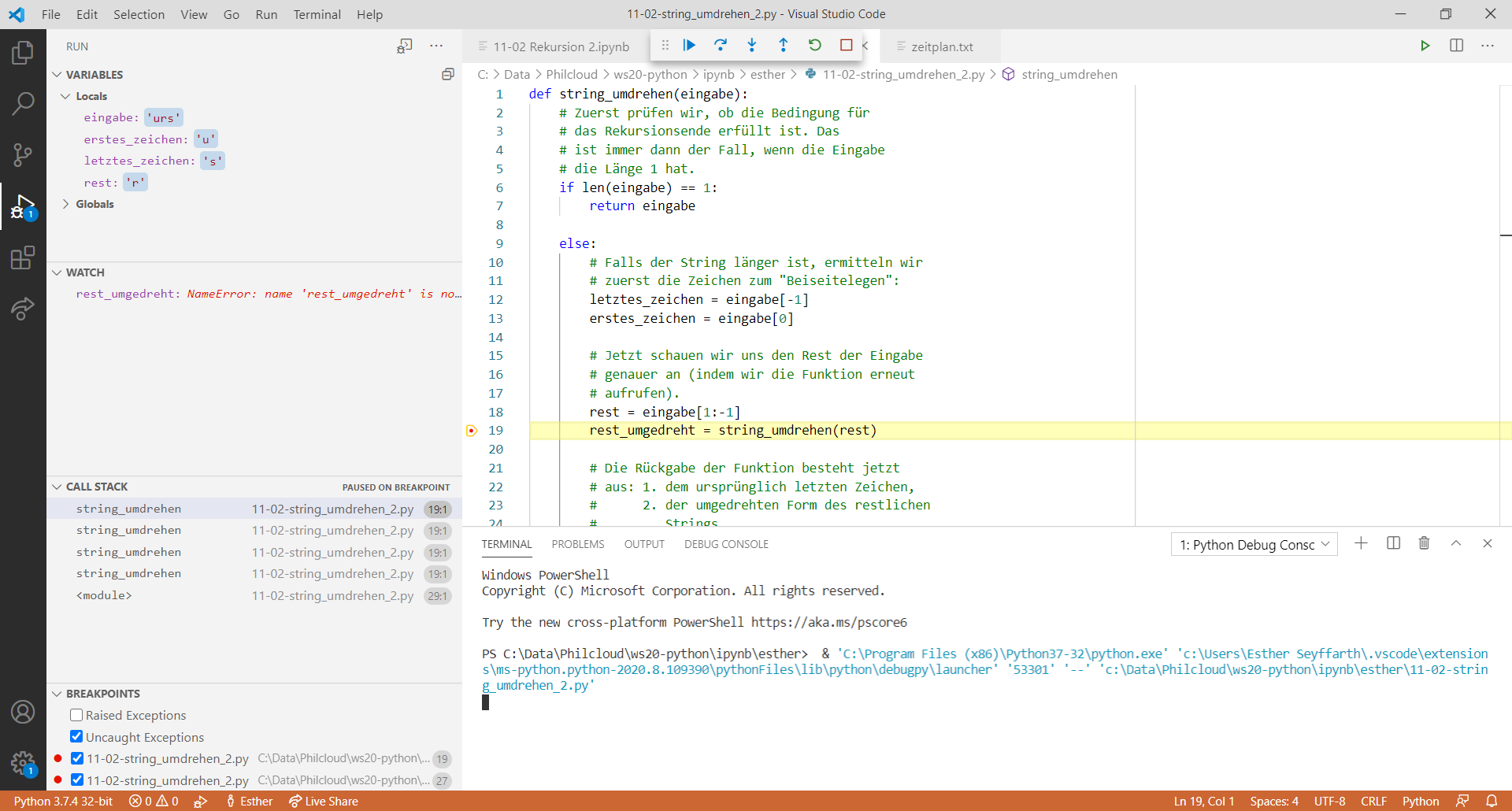
Die Funktion, die die oben aufgelisteten Schritte allgemein definiert, sieht etwa so aus:

def string_umdrehen(eingabe):
    # Zuerst prüfen wir, ob die Bedingung für
    # das Rekursionsende erfüllt ist. Das
    # ist immer dann der Fall, wenn die Eingabe
    # die Länge 1 hat.
    if len(eingabe) == 1:
        return eingabe

    else:
        # Falls der String länger ist, ermitteln wir
        # zuerst das Zeichen zum "Beiseitelegen":
        naechstes_zeichen = eingabe[-1]

        # Jetzt schauen wir uns den Rest der Eingabe
        # genauer an (indem wir die Funktion erneut
        # aufrufen).
        rest = eingabe[:-1]
        rest_umgedreht = string_umdrehen(rest)

        # Die Rückgabe der Funktion besteht jetzt 
        # aus: 1. dem ursprünglich letzten Zeichen,
        #      2. der umgedrehten Form des restlichen
        #         Strings.
        zwischenergebnis = naechstes_zeichen + rest_umgedreht
        print(zwischenergebnis)
        return zwischenergebnis

print(string_umdrehen("Rekursion"))

Um uns den Ablauf dieses Programms näher anzuschauen, können wir den Code in einer Pythondatei speichern und einen Breakpoint setzen, um während der Laufzeit den Interpreter zu pausieren. Dann sehen wir, wie sich die Werte der Variablen verändern und wie nach und nach das Ergebnis zusammengesetzt wird. Dafür ist es eine gute Idee, den Breakpoint genau in die Zeile zu setzen, an der die Funktion sich selbst aufruft (hier: Zeile 18). Außerdem interessieren wir uns für den Inhalt der Variable zwischenergebnis und setzen daher einen weiteren Breakpoint in Zeile 25.

Nachdem wir den Debugger starten, sehen wir die folgende Ansicht. Die Variablen naechstes_zeichen und rest enthalten genau die Teilstrings, die wir oben in unserem Beispiel ebenfalls ermittelt hatten.

Der Debugger hat eben angehalten, bevor die Funktion sich selbst aufgerufen hat. Weil wir wissen wollen, wie die Rekursion abläuft, wählen wir jetzt den Debugger-Knopf "Step into". Damit folgen wir dem Interpreter in den Funktionsaufruf hinein. Wir sehen, dass der Wert für eingabe jetzt den gleichen Teilstring enthält wie im letzten Schritt die Variable rest; das ist nicht verwunderlich, denn wir haben die Funktion ja mit dem Argument rest aufgerufen. Werte für naechstes_zeichen und rest sind innerhalb des jetzt aktuellen Funktionsaufrufs noch nicht bekannt, weil wir uns noch am Anfang der Funktion befinden.

Eine weitere Veränderung zwischen dem letzten Schritt und dem jetzt aktuellen Schritt ist der Call Stack an der linken Seite. Der Stack enthält die Information, in welcher Verschachtelung wir die verschiedenen Funktionen aufgerufen haben. Im ersten Screenshot war nur ein Aufruf von string_umdrehen zu sehen. Da wir jetzt in den rekursiven Aufruf der Funktion eingestiegen sind, ist ein neuer Aufruf von string_umdrehen ergänzt worden. Die Zahl neben dem Funktionsnamen zeigt uns, dass der erste Aufruf gerade in Zeile 18 steht, wir uns im aktuellen Aufruf aber in Zeile 6 befinden. Sobald der jetzt aktuelle Aufruf der Funktion ordnungsgemäß beendet ist, wird die Funktion wieder vom Call Stack entfernt.

Ein Klick auf "Continue" bringt uns weiter zu Zeile 18, diesmal mit anderen Variablenwerten. Vom "n" am Ende des ursprünglichen Eingabewortes "Rekursion" ist hier jetzt gar nichts mehr zu sehen: Wir befinden uns in einem abgekapselten, verschachtelten Funktionsaufruf, der nur das Teilwort "Rekursio" kennt.

Ein weiterer Klick auf "Continue" bringt uns nicht etwa in Zeile 25, sondern wieder in Zeile 18. Warum? Wir schaffen es nicht, bis zum Ende der Funktion durchzulaufen, weil in Zeile 18 ja ein rekursiver Funktionsaufruf steht, der uns wiederum zu Zeile 18 der nächsten Verschachtelungsebene bringt. Je häufiger wir diesen Sprung in die Funktionsaufrufe hinein machen, umso mehr wächst auch unser Call Stack:

Ab jetzt führt jeder Klick auf "Continue" dazu, dass wir in Zeile 25 springen; das ist dann jeweils das Ende der verschachtelten Funktionen, und beim nächsten Schritt erreichen wir dann das Ende der Funktion, in der zuletzt die Rekursion ausgelöst wurde. Wir erkennen das auch daran, dass der Call Stack immer kleiner wird. Außerdem erhalten wir jetzt schrittweise mehr Informationen zum jeweiligen Wert von zwischenergebnis.

Je weiter wir die Verschachtelungen der Rekursionsschritte wieder auflösen, indem wir die Funktionen nach und nach verlassen, umso länger wird auch unser Zwischenergebnis. Schließlich enthält der Call Stack nur noch ein einziges Element. Das ist dann der Funktionsaufruf, dessen Zwischenergebnis gleichzeitig das Endergebnis der Rekursion ist. Wir haben den String nach und nach immer kleiner gemacht, die Funktion immer wieder für die jeweils kleineren Teilstrings aufgerufen, dann pro Rekursionsschritt ein Zwischenergebnis zurückgegeben und die Zwischenergebnisse mit den beiseite gelegten Zeichen konkateniert; zum Schluss konkatenieren wir das Zwischenergebnis mit dem Zeichen, das wir ganz am Anfang beiseite gelegt haben, nämlich mit dem "R". Dann gibt die Funktion ihr Endergebnis zurück und die Rekursion ist beendet. In unserem Programm erfolgt zuletzt ein print()-Aufruf, in dem wir das Gesamtergebnis ausgeben.

Rekursionsschritte reduzieren

Weil unser Eingabewort "Rekursion" 9 Zeichen hat und wir die Funktion so oft aufrufen, bis wir es nur noch mit einem einzigen Zeichen zu tun haben, enthält unsere Rekursion 8 Schritte. Das ist eine ganze Menge für so eine triviale Aufgabe.

Manchmal können wir durch kluge Veränderungen die Anzahl der benötigten Rekursionsschritte reduzieren. Rekursion verbraucht relativ viel Arbeitsspeicher, deshalb sollten wir uns immer Gedanken machen, ob wir die Anzahl der Funktionsaufrufe verringern können.

In unserem Beispiel haben wir jeweils das letzte Zeichen des Strings beiseite gelegt. Wir können den Code so verändern, dass jeweils das erste und das letzte Zeichen beiseite gelegt werden. Wir müssen dann nur daran denken, die Zwischenergebnisse in der richtigen Reihenfolge zusammenzufügen:

1. Endergebnis für string_umdrehen("Rekursion"): "n" + Zwischenergebnis für "ekursio" + "R"
2. Zwischenergebnis für string_umdrehen("ekursio"): "o" + Zwischenergebnis für "kursi" + "e"
3. ...
4. Zwischenergebnis für string_umdrehen("r"): "r" (Rekursionsende!)

Der veränderte Code sieht jetzt folgendermaßen aus:

def string_umdrehen(eingabe):
    # Zuerst prüfen wir, ob die Bedingung für
    # das Rekursionsende erfüllt ist. Das
    # ist immer dann der Fall, wenn die Eingabe
    # die Länge 1 hat.
    if len(eingabe) <= 1:
        return eingabe

    else:
        # Falls der String länger ist, ermitteln wir
        # zuerst die Zeichen zum "Beiseitelegen":
        letztes_zeichen = eingabe[-1]   # n
        erstes_zeichen = eingabe[0]     # R

        # Jetzt schauen wir uns den Rest der Eingabe
        # genauer an (indem wir die Funktion erneut
        # aufrufen).
        rest = eingabe[1:-1]
        rest_umgedreht = string_umdrehen(rest)

        # Die Rückgabe der Funktion besteht jetzt 
        # aus: 1. dem ursprünglich letzten Zeichen,
        #      2. der umgedrehten Form des restlichen
        #         Strings,
        #      3. dem ursprünglich ersten Zeichen.
        zwischenergebnis = letztes_zeichen + rest_umgedreht + erstes_zeichen
        return zwischenergebnis

print(string_umdrehen("Rekursion"))

Hier werden sowohl das erste als auch das letzte Zeichen beiseite gelegt, und deshalb schrumpft der String schneller und innerhalb weniger Rekursionsschritte. So sieht das zu Beginn aus:

Wenn wir die Mitte des Strings (und damit die Abbruchbedingung) erreichen, sieht der Call Stack so aus:

Ab jetzt erhalten wir beim Klick auf "Continue" die Zwischenergebnisse, die entstehen, wenn man den String von innen nach außen umdreht:

Beide Ansätze sind valide Lösungen, wenn es darum geht, mithilfe von Rekursion einen beliebigen String umzudrehen. Der zweite Ansatz braucht weniger Rekursionsschritte, weil der String von beiden Seiten gleichzeitig bearbeitet wird. Bei sehr umfangreichen Aufgaben ist es hilfreich, wenn man die Rekursionsschritte möglichst weit reduziert.

Zusammenfassung

Mit dem Debugger können wir leichter nachverfolgen, welche Funktionsaufrufe mit welchen Argumenten in welcher Reihenfolge ablaufen. Es ist auch hilfreich, die Zwischenergebnisse zu beobachten, die nach und nach zum Endergebnis zusammengefügt werden.

Beim Schreiben rekursiver Funktionen empfehlen wir die folgenden Vorgehensweisen:

• Für ein übersichtliches Beispiel die einzelnen Schritte manuell durchspielen.
• Klare Definition der Abbruchbedingung finden (hier: wenn der String nur noch ein Zeichen enthält).
• Innerhalb der Funktion immer zuerst die Abbruchbedingung prüfen; nur wenn sie nicht erfüllt ist, lösen wir den nächsten Rekursionsschritt aus.
• Großzügig debuggen: Wenn wir Schritt für Schritt durch das Programm durchklicken, sehen wir genau, welche Informationen bei jedem rekursiven Funktionsaufruf anfallen und wo eventuelle Probleme auftreten.
• Falls möglich, auf eine geringe Rekursionstiefe achten. Hier haben wir das erreicht, indem wir den String von beiden Seiten aus betrachten.

Weitere Themen dieser Woche:

• 11-01: Rekursion I